Noções sobre números
Proporcionalidade direta- Exercício

Noções sobre Funções
Funções
2.
2.1 Indica:
2.1.1
O domínio da função f _______________________________
2.1.2
O contradomínio da função f __________________________
2.1.3
O conjunto de chegada da função f ____________________
2.2
Qual é a imagem do objeto – 1? _____________________________
2.3. Quais são os objetos que têm como
imagem 2? ________________
|
|
|
|
|
|
Classificação de ângulos
Noção de ângulo adjacente, complementar e suplementar
Dois ângulos são suplementares quando a soma de suas medidas é 180º
Dois ângulos são complementares quando a soma de suas medidas é 90º.
Dois ângulos são adjacentes quando são consecutivos e não possuem pontos internos comuns.
Cá vai mais um teste... Alguns conceitos sobre ângulos, propriedades de triângulos
Problemas com Equações do 1.º Grau
As equações do 1.º grau são essenciais para o desenvolvimento do raciocínio lógico e da capacidade de resolução de problemas matemáticos. Abaixo encontras alguns problemas práticos que te ajudam a consolidar este tema.
Problema 1
Sabendo que a diferença entre o dobro de um número e a sua quinta parte é igual à soma desse número com 1, determina o número.
Problema 2
Resolução de equações com parenteses
Resolve as seguintes equações do 1.º grau
Resolve cada uma das equações, apresentando todos os passos da resolução.
a)
b)
c)
d)
e)
f)
g)
Pode-se esquematizar uma regra prática para a resolução destas equações:
2. Equações simples com variáveis em ambos os membros
a)
b)
c)
3. Equações com números decimais
a)
b)
c)
4. Equações com frações
a)
b)
c)
Exemplo de uma resolução de uma equação simples de 1º grau
Regras de operações com potências
- Adição e subtracção
- Multiplicação de potências
- Divisão de potências
Para dividir potências com a mesma base, diferente de zero, mantém-se a base e subtraem-se os expoentes.
- Potência de potência
- Potência de expoente nulo
















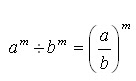


Sem comentários:
Enviar um comentário